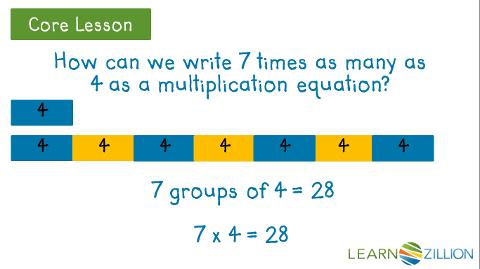Multiplicative Comparisons
| parent_overview_unit_6_multiplicative_comparisons.docx | |
| File Size: | 23 kb |
| File Type: | docx |
Standards:
4.0A.1 Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 × 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations.
4.OA.2 Multiply or divide to solve word problems involving multiplicative comparison, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison.
Important Notes from NC Unpacking Document:
4.0A.1 Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 × 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations.
4.OA.2 Multiply or divide to solve word problems involving multiplicative comparison, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison.
Important Notes from NC Unpacking Document:
- When distinguishing multiplicative comparison from additive comparison, students should note that Additive comparisons focus on the difference between two quantities (e.g., eb has 3 apples and Karen has 5 apples. How many more apples does Karen have?). A simple way to remember this is, "How many more?"
- Multiplicative comparisons focus on comparing two quantities by showing that one quantity is a specified number of times larger or smaller than the other (e.g., Deb ran 3 miles. Karen ran 5 times as many miles as Deb. How many miles did Karen run?). A simple way to remember this is "How many times as much?" or "How many times as many?"
Comparison BarsLinks
|
Helpful KnowledgeIn this shorter unit, students practice reading word problems/situations and writing equations with variables. The situations involve a multiplicative comparison, meaning they need to be able to multiply or divide to determine an unknown value.
Examples:
(6 x 3 = g; g = 18 feet)
| ||||||