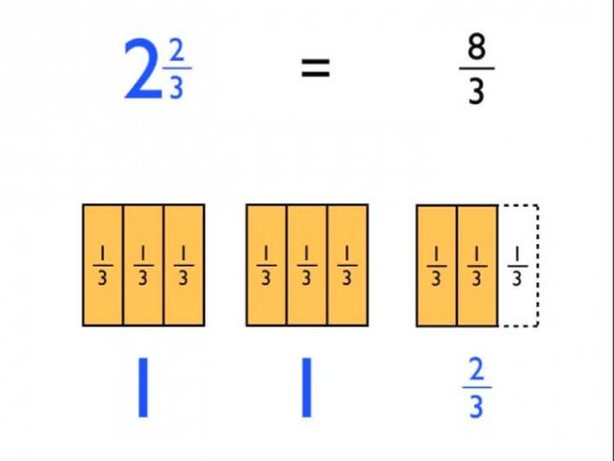
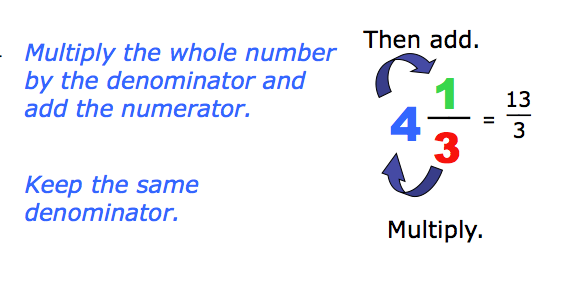
Equivalent Fractions
| Parent Letter-Equivalent Fractions | |
| File Size: | 25 kb |
| File Type: | docx |
Standards:
5.NF.1
Explain why a fraction a/b is equivalent to a fraction (n ×a)/(n × b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to recognize and generate equivalent fractions.
5.NF.3
Understand a fraction a/b with a >;; 1 as a sum of fractions 1/b. a. Understand addition and subtraction of fractions as joining and separating parts referring to the same whole. b. Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. Examples: 3/8 = 1/8 + 1/8 + 1/8; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8. c.
Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction. d. Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.
5.NF.1
Explain why a fraction a/b is equivalent to a fraction (n ×a)/(n × b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to recognize and generate equivalent fractions.
5.NF.3
Understand a fraction a/b with a >;; 1 as a sum of fractions 1/b. a. Understand addition and subtraction of fractions as joining and separating parts referring to the same whole. b. Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. Examples: 3/8 = 1/8 + 1/8 + 1/8; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8. c.
Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction. d. Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.